【非データサイエンティスト向け】階層ベイズのイメージと使いどころ

　リブセンスでデータサイエンティストをしている北原です。今回は階層ベイズという技術について、非データサイエンティスト向けに解説します。検索すれば技術の詳細や実行方法についての素晴らしい解説がたくさん見つかるので、ここでは使われ方のイメージと使うと有効な場面を中心に紹介します。リブセンスでは階層ベイズを組み込んだ機能を実運用し始めて5年以上経過しているので、過去使われていたものを中心に実用例も紹介します。

　階層ベイズモデルというのは、ざっくり言うと、個人のような小さい粒度のモデルの全体傾向を大きい粒度のモデルで表現したベイズ統計モデルの総称です。データや問題に合わせて様々な階層ベイズモデルを作ることができるので応用範囲が非常に広いです。しかし、機械学習ライブラリに組み込まれているような具体的な固有のモデルを指すものではないので、わかりにくい部分もあります。本記事では階層ベイズが有用ないくつかの例を取り上げて、階層ベイズを使うことでどのような実務上の課題を解決できるのかを説明します。

ユースケース

　階層ベイズが有用なケースをいくつか紹介します。ここでは推定したいもの別に、連続値の平均、比率、回帰モデルの係数・切片を推定するケースを取り上げます。弊社は人材サービスを中心に運営しているので、人材サービスでのユースケースについて考えます。

例1：企業別の想定提示年収（平均値）

　一つ目のケースは、階層ベイズを使わなくても実用上問題ないことが多いのですが、例としては比較的わかりやすいので紹介します。

状況

　転職エージェントなど採用時の年収に一定比率を乗じた金額が売上になる成果報酬型サービスについて考えます。提示年収の水準は企業によって大きく異なることがありますし、同じ企業でも提示年収が大きくばらつくことがあります。企業別に想定提示年収金額を推定し、推定金額が高い企業ほどサポートを手厚くすることで売上の最大化を試みたとしましょう。実際には予定採用人数や採用率なども関係してきますが、ここでは問題を簡単にするために想定提示年収のみが問題になっていたとします。また、内定実績がない企業は対象外とします。また、企業全体の平均的な提示年収についても知りたいとします。

　基本的には、過去の提示年収のみしか使えない状況を考えます。業種や職種によって提示年収は異なりますが、同一業種や同一職種でも企業によって提示年収は異なりますし、同じ業種内あるいは職種内で提示年収がどの程度になるのかを知りたいものとします。こういう状況では機械学習が使われるのだから非現実的な設定ではと思う人もいるかもしれませんが、既存の属性情報に加えて過去実績を利用して精度を上げることもあります。

　問題になるのは過去の提示年収データが少ない企業です。大企業のような内定実績が多い企業については過去の実績から比較的正確な提示年収の水準を知ることができます。一方で、中小企業や新たにサービスを使い始めた企業は過去の提示年収データがほとんどないため、得られている一部の過去実績に過度に依存してしまうという問題があります。

　特に問題になるのは、平均より過度に高いあるいは低い提示年収を出した企業です。少ないデータのみを参考に、それらの企業を提示年収が高いあるいは低い企業とみなすこともできます。その場合、内定実績が少ない企業は極端な扱いを受けやすくなるので不都合が生じることがあります。

　さらに付け加えると、平均提示年収の計算にも注意が必要なことがあります。そのまま計算すると内定実績の多い企業の影響が多くなります。逆に、企業ごとの平均を計算した後に全体平均を計算すると、内定実績が少ない企業が出した過度な提示年収の影響を受けやすくなります。大企業の影響も受けすぎず、一部の過度な提示年収の影響も受けすぎずに平均を計算できるのが望ましいです。

グラフ

　文章だけではイメージがつきにくいと思うので、グラフで確認してみましょう。以下は、上図が提示年収のサンプルを作成してヒストグラムにしたもので、下図が企業別に提示年収をそのまま平均してヒストグラムにしたものです。提示年収の平均が高い企業(平均705万)と低い企業(平均496万)を別の色で表示しています。

例：企業別提示年収のヒストグラム

この例で課題になっているのは、このとき一回だけ年収750万を提示したことのある企業や450万を提示した企業を平均提示年収いくらの企業として扱うのがよいかというものです。一回だけの実績で、従来企業より平均提示年収が高いあるいは低いと推定するのはやりすぎな気がします。では、どの程度の提示年収として扱うのがよいでしょうか。

データ

　具体的なデータフォーマットは以下のようなものになります。

id	提示年収
1	581
1	619
2	649
2	592
2	533
2	677
2	622
3	570
3	554
4	623

問題設定

　まとめると以下のようになります。

• データ
  • カラム
    • 企業ID
    • 提示年数(数値)
  • 1社につき複数の数値データ
  • 同一企業でも提示年数は大きくばらつく
  • 企業によって平均値は大きく異なる
  • 1社あたりの実績データ数は多いケースも少ないケースもある
• 目的
  • 各社の平均と全体平均の算出
• 課題
  • データが少ない企業の妥当な平均を推定
    • 異常値を抑制
  • データの多い企業や少ない企業の影響を受けすぎずに全体平均を推定

例2：求人別の採用率（比率）

　比率データの階層ベイズについてはAnalytics Blogの記事でも紹介したのですが、階層ベイズの有用性がわかりやすいのでここでも取り上げます。

analytics.livesense.co.jp

状況

　成果報酬型求人サービスでは採用率も重要なので、求人別の採用率を推定するケースについて考えます。採用率がわかると集客やレコメンデーション、営業など幅広く活用することができます。例1との大きな違いは推定対象です。例1では平均値が推定対象でしたが、例2では比率です。推定対象以外は例1と似た状況を考えます。ここでも全体の採用率も知りたいものとします。推定に使えるデータは、求人別の採否です。このケースでも他の属性は利用できないものとします。

　採用率の推定でも問題になるのはデータが少ないケースです。応募数が少ないと、そのまま計算するだけでは異常な採用率になってしまいます。例えば、応募数が1件の場合、採用率は0%か100%になってしまいます。2件以上の場合であっても応募数が少ないと推定採用率の上振れ下振れが発生しやすくなります。応募数が少ないほど異常な推定値になりやすいですが、何件応募があればそのまま計算した採用率を使ってよいのかもわかりにくいです。

　このとき応募が少ない求人でも妥当な採用率を推定するのが課題です。また、応募数が多すぎるあるいは少なすぎる求人の影響を過度に受けない全体平均採用率を推定するのも課題です。

グラフ

　以下は、採否のサンプルを作成して求人ごとに採用率を計算しヒストグラムにしたものです。応募数の少ない求人の影響で採用率が0%、50%、100%の数が多くなっていることがわかります。

例：求人別採用率のヒストグラム

この例で課題になっているのは、応募数が少ない求人の採用率をどう扱うのがよいかというものです。例えば、応募数1件採用1件の求人の採用率をどの程度と推定するのがよいでしょうか。また、単純計算して採用率0%であった求人でも応募数が増加した時にわかる本当の採用率は異なりそうです。応募数1件で採用0件の求人より応募数2件で採用0件のほうが採用率が低い可能性が高そうです。では、それぞれをどの程度の採用率として扱うのがよいでしょうか？

データ

　具体的なデータフォーマットは以下のようなものになります。

id	採否
1	0
1	0
2	1
2	0
2	0
3	0
4	0
4	0
4	0
4	0

問題設定

• データ
  • カラム
    • 求人ID
    • 採否(採用されたら1されなかったら0)
  • 求人によって採用率が大きく異なる
  • 1求人あたりの応募数は多いケースも少ないケースもある
• 目的
  • 各求人の採用率と全体平均採用率の算出
• 課題
  • 応募数が少ない求人の妥当な採用率を推定
    • 異常値を抑制する
  • 応募数の多い求人や少ない求人の影響を受けすぎずに全体平均採用率を推定

例3：企業別の高評価特徴（回帰モデルの係数・切片）

　この例は回帰モデルの係数や切片の計算に階層ベイズを必要とするケースで、多くの文献で階層ベイズモデルとして紹介されることが多いものです。

状況

　企業風土に合うかやスキルなど企業によって高く評価することが異なることがあるので、どのような特徴がある求職者に高い年収を提示するかを推定するケースについて考えてみましょう。そのような特徴は多数ありますが、ここでは簡単にするため何らかのスキル診断の点数のみ考えます。企業によってスキル点数を重視するところと重視しないところがあるので、これらを推定したいとします。推定対象以外は例1と似た状況を考えます。推定に使えるデータは、提示年収とスキル点数(平均0分散1に正規化済み)です。このケースでも他の属性は利用できないものとします。

　例3は例1や例2より少し複雑なケースで単回帰を考えます。単回帰は「提示年収 = スキル重視度 ✖️ スキル点数」という形になります。スキル重視度が算出したいもので、この式はスキル重視度が大きいほどスキル点数が提示年収に大きく反映されることを表しています。

　この例でも問題になるのはデータが少ないケースです。データ量が十分にあれば正確な推定値を計算できるのですが、データ量が少ないと不正確な推定値になりやすくなりますし異常値が得られることも少なくありません。また極端なケースではありますが過去の実績データが1件しかない場合は推定を実行することすらできません。

　課題は、実績データが少ない企業の妥当なスキル重視度を推定することと、過去実績が多すぎるあるいは少なすぎる企業の影響を過度に受けずに全体平均のスキル重視度を推定することです。

グラフ

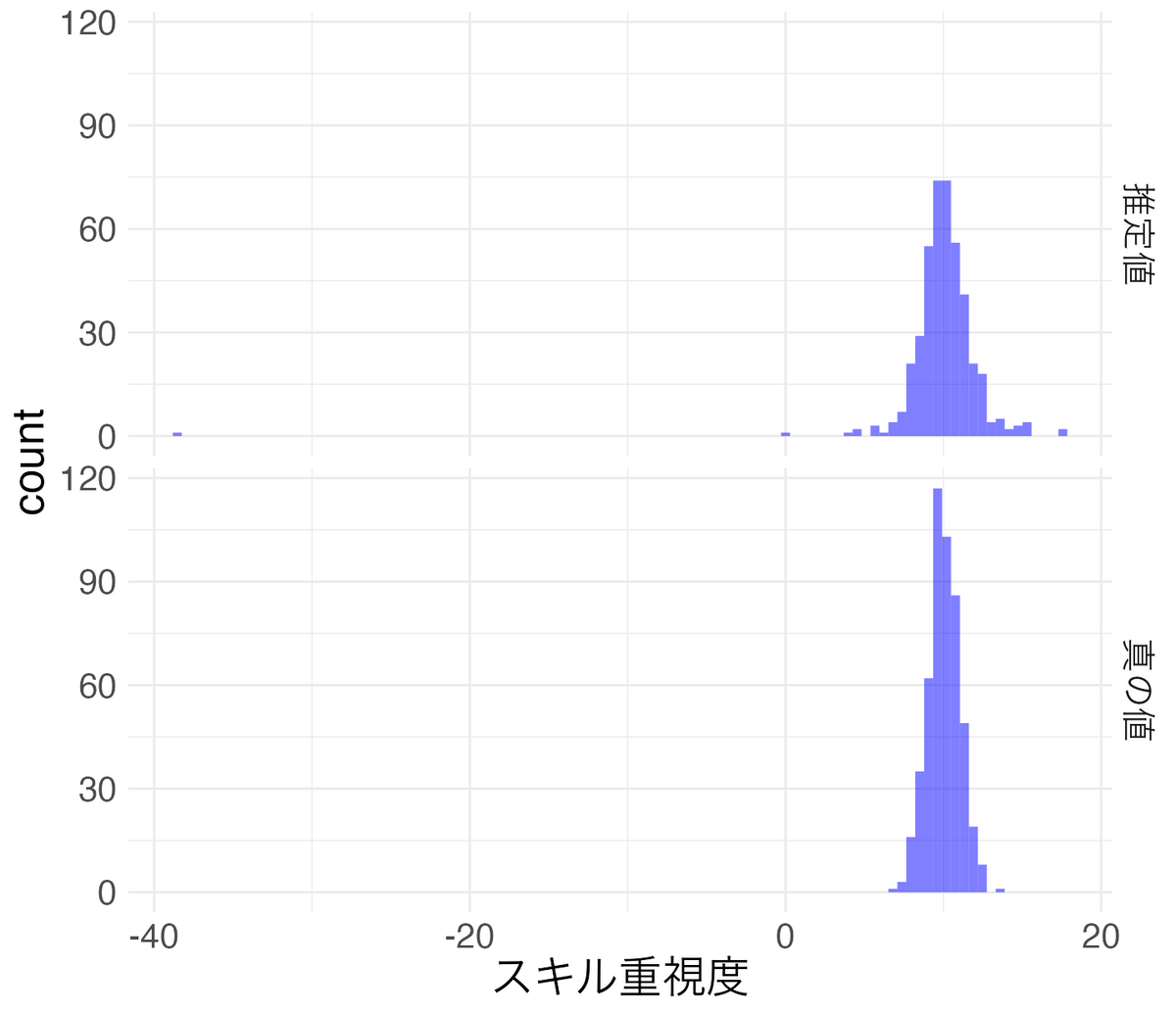
　以下は、提示年収とスキル点数のサンプルを作成して企業ごとにスキル重視度を計算しヒストグラムにしたものです。推定されたスキル重視度とサンプル作成に利用したスキル重視度(真の値)を表示しています。ただし、データ数が1つしかない企業ではスキル重視度を計算できないので削除しています。このサンプルの生成では各企業のスキル重視度を平均10分散1で生成し、さらに企業別に個々のスキル重視度を企業別スキル重視度を平均とし分散1で生成しています。

例：スキル重視度のヒストグラム

推定値では異常値が見られることと、真の値と比較して推定値は裾が広がっていることが確認できます。このサンプルは乱数で生成したきれいなデータなので推定値は比較的安定しています。しかし、実務で扱うデータでは推定値が大きくばらつき異常値も大量に発生することが多いです。さらにいうと、単純平均などと比較して回帰モデルのほうが複雑な推定を行うので、ノイズの多いデータではデータ量が比較的多めでも推定値がばらつきやすいです。

　この例の課題は異常値を抑制して妥当なスキル重視度を推定することです。さらに、できれば過去実績が1件の企業についても推定できることが望ましいです。また、過去実績が多すぎるあるいは少なすぎる企業の影響を過度に受けずに全体平均スキル重視度を推定するのも課題です。

データ

id	スキル点数	提示年収
1	1.135	610
1	1.112	608
1	-0.871	592
1	0.211	600
2	-1.247	587
2	0.998	608
2	-0.541	593
3	0.351	603
4	-0.591	592
4	-1.334	585

問題設定

• データ
  • カラム
    • 企業ID
    • 提示年収
    • スキル点数(平均0分散1に正規化済み)
  • 企業によってスキル重視度が大きく異なる
  • 1企業あたりの実績データ数は多いケースも少ないケースもある
• 目的
  • 各企業のスキル重視度と全体平均スキル重視度の算出
• 課題
  • 実績データが少ない企業の妥当なスキル重視度を推定
    • 異常値を抑制する
  • 実績データの多い企業や少ない企業の影響を受けすぎずに全体平均スキル重視度を推定

階層ベイズのイメージ

少しだけ確率分布の話

　モデルは確率分布を使って表現されるので、少しだけ確率分布の説明をします。理解して欲しいのは2点だけです。一つ目は確率分布には特徴の異なる複数のものがあるということです。二つ目は確率分布にはその分布を確定させるパラメータがあるということです。

確率分布には特徴の異なる複数のものがある

　確率分布には様々なものがあり、モデルを考える時はデータや目的に合わせて適切なものを選びます。確率分布の条件を満たしていれば、自分で確率分布を定義してモデルを作成することもあります。

　どんな確率分布があるか、ざっと見てみましょう。

種類の異なる確率分布の例

左のグラフは代表的な確率分布である正規分布です。左右対称の釣鐘型の形状をしていて裾が長くなっていることがわかります。これは平均0の正規分布なので0になる確率が一番高く、0から離れるほど確率が低くなることを表しています。右のグラフはベータ分布と呼ばれるものです。左右非対称で0から1までの値をとる分布です。この分布は0.3の確率が一番高く0もしくは1に近づくと急速に確率が低くなることを表しています。

確率分布にはその分布を確定させるパラメータがある

　確率分布の種類が同じでも、パラメータが異なると分布形が変わります。ここでいうパラメータというのは確率分布を特徴づける変数です。

　例えば、正規分布は平均と分散のパラメータをもっています。次のグラフは左から平均-1分散1、平均0分散1、平均0分散2の正規分布を示したものです。平均パラメータが変わると分布形状は変わらないですがx軸方向に移動していることがわかります。分散パラメータが変わると分布の横幅が変わっていることがわかります。

パラメータの異なる確率分布の例

少しだけモデル作成の話

　階層ベイズモデルはモデルを組み合わせることで表現するので、モデルを作成するということについて少しだけ説明をします。ここでいうモデル作成というのは、データを表現する確率分布を決めることです。モデル作成では、モデル設計とパラメータ推定を行います。

　モデル設計というのは、データの特徴を表現するのに、どの確率分布をどのように組み合わせるのかを決めることを指します。このとき確率分布のパラメータから最終的に知りたいことを算出できるようにします。確率分布を決めただけでは分布は確定しませんが、対称性や裾の長さなど取りうる形状が限定されるので、モデルの特徴がほぼ決まります。モデル設計はデータや目的に合わせて行います。

　パラメータ推定というのは、得られているデータを使ってモデル設計で決めたパラメータの値を算出します。これによってデータを表現する確率分布が決まります。データやモデルによってはパラメータをうまく計算できないことがあるので、その場合はモデル設計からやり直したりします。

　イメージとしては以下のような感じです。モデル設計で分布の種類を決めて、パラメータ推定で分布の形をデータにフィットさせる。

モデル作成のイメージ

階層ベイズの基本的な考え方

　冒頭で、階層ベイズモデルは、小さい粒度のモデルの全体傾向を大きい粒度のモデルで表現したものという説明をしましたが、ポイントは小さい粒度のモデルと大きい粒度のモデルが一つのモデルで表現されているというところです。これによって、個別のデータが少なくて小さい粒度のモデルの推定が難しいときでも、大きい粒度のモデルの情報で安定した推定ができるようになります。小さい粒度のモデルの全体傾向を大きい粒度のモデルで表現するというのは、小さい粒度のモデルの全体傾向に制約をつけているという捉え方もできます。

　大きい粒度のモデルの情報は、小さい粒度のモデルのデータ量が少ないほど多く使われます。逆に、小さい粒度のモデルのデータ量が多くなるほど大きい粒度のモデルの情報は使われなくなります。これによってデータ量に応じたバランスのよい推定が可能になります。

　小さい粒度のモデル、大きい粒度のモデルという表現は煩雑なので、ここからはそれぞれ個別モデル、全体モデルと表現します。また、ユースケースの例では小さい粒度の単位が企業であったり求人であったりしましたが、これを個体と表現します。

　イメージとしては以下のような感じです。個体ごとに独立してデータから個別モデルを作成しようとするとデータ量が少なくて失敗し　しかし、階層ベイズでは全体構造の情報を利用することでデータが少ない個体についてもモデルを作成することができます。

階層ベイズのイメージ

例1：企業別の想定提示年収

　ここからは、各ユースケースで階層ベイズがどのように働くのかを見てみましょう。

　この例では、個別モデルは企業別の提示年収を推定するモデル、全体モデルは企業別提示年収の全体傾向を表すモデルが考えられます。

　階層ベイズを使うと、平均より過度に高いあるいは低い提示年収を出した企業がどのように扱われるかを考えてみましょう。過去実績が少ないと全体モデルの影響が大きくなるので、全体平均に近い値が推定されます。例えば、全体平均が600万のとき、750万を1回提示しただけだと平均提示年収690万などと推定されます。しかし、データが多くなると徐々に個別モデルの影響が強くなってきます。例えば、750万を3回提示すると高年収企業の可能性がかなり高くなるので平均提示年収730万などと推定されます。このように個別モデル作成に使われたデータ量に応じて個別モデルと全体モデルの影響が調整されるので、データが少ない時に起こりがちな、平均より過度に高いあるいは低い提示年収の影響を抑制することができます。

例2：求人別の採用率

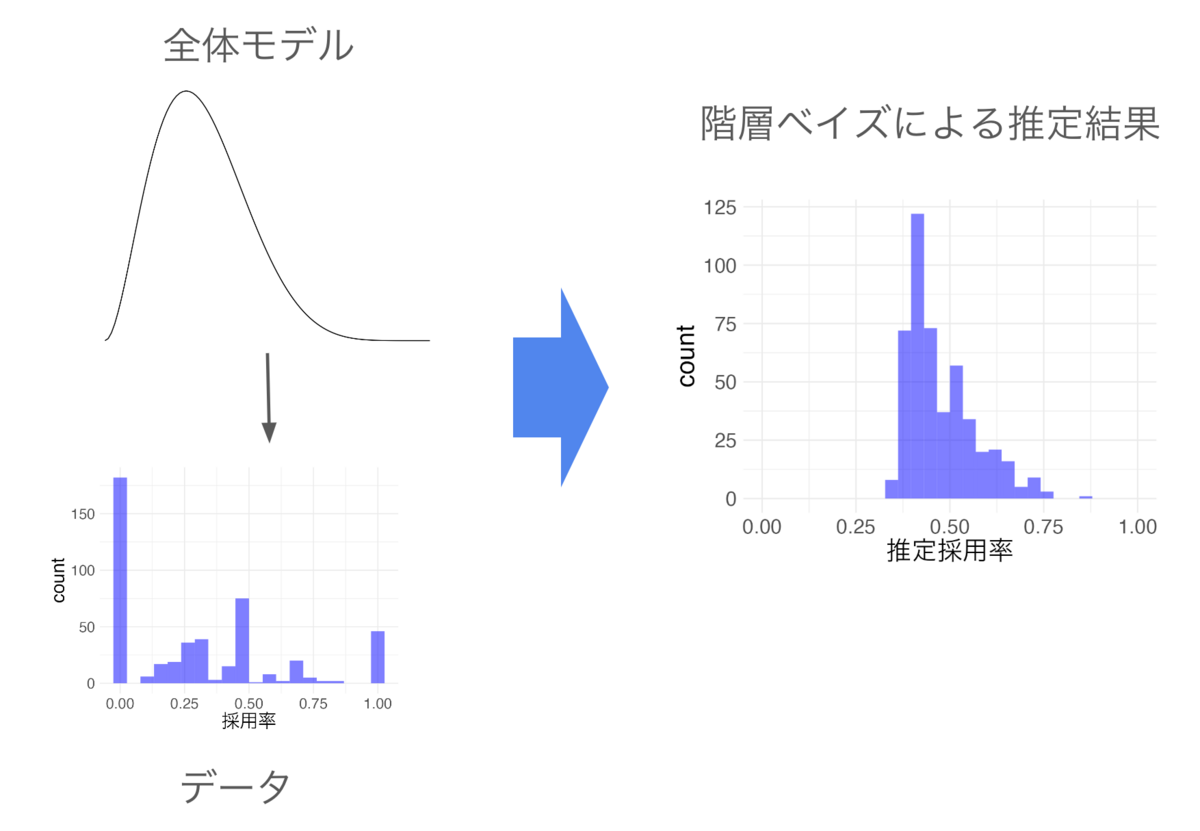
　この例では、個別モデルは求人別採用率を推定するモデル、全体モデルは求人別採用率の全体傾向を表すモデルです。比率を階層ベイズで推定すると、そのまま比率を計算した時と比較してわかりやすい変化をします。実際にサンプルデータの推定をしたものは以下のようになります。

階層ベイズによる比率の推定の例

　階層ベイズを使うと、応募数が少ない求人の採用率がどのように推定されるか考えてみましょう。例えば、全体の採用率が30%のとき、応募1件採用1件の求人は採用率42%などと推定されます。そのまま計算すれば採用率100%ですが、全体採用率が30%だと偶然の可能性が高いので全体平均よりは高いですが、そのまま計算した結果よりは低く算出されます。データ量が増えると個別モデルの影響が大きくなります。例えば、応募2件採用2件になると、採用率が高くなる可能性が高まるので採用率53%などと算出されます。もし全体の採用率が10%だった場合は、30%の時と比較して求人別採用率も低く算出されます。例えば、 応募1件採用1件の求人は採用率は31%などと推定されます。つまり、求人別採用率は個別の結果だけでなく、データ量に応じて全体モデルの影響を受けて推定されます。これによって、全体傾向から乖離した異常な採用率が算出されにくくなります。

例3：企業別の高評価特徴

　この例では、個別モデルはスキル点数から提示年収を推定するモデル、全体モデルは企業別スキル重視度の全体傾向を表すモデルです。階層ベイズを使うことによって、企業別スキル重視度推定値が安定し異常値を抑制することができます。さらに、モデルをうまく作ることができると、個別モデルの生成に使うデータが1件しかない場合でも企業別スキル重視度を推定することができます。また、階層ベイズを使ってもデータが少ない場合は推定結果の信頼性は落ちますが、どの程度信頼できるかを確率として示すこともできます。

階層ベイズの使いどころ

　本節では、実務で利用することを想定した階層ベイズの利用用途と使いどころを判断するためのポイントについて説明します。

利用用途

　階層ベイズの主な利用用途は「パラメータの安定化」と「全体傾向の正確な推定」の二つだけです。細かいことを言えば他にもありますが、基本はこの二つです。さらにいうと、実務では「パラメータの安定化」で使うことがほとんどです。

パラメータの安定化

　実務で運用する場合は、パラメータ推定の安定化のために利用するケースが多いです。個体別に推定すると正確なパラメータ推定ができないけれども全体傾向はある程度わかっているときに、全体傾向の情報を使ってデータ量の少ない個別モデルのパラメータ推定を行うのに使います。

　実務で遭遇する場面では、普通は推定を諦めるような場面で使うことが多いです。例えば、例2で応募数1件のデータから採用率を推定するケースを考えていますが、かなり無茶なことをしているのがわかると思います。従来はデータ量が少ない個体については適切な対応が難しく、施策の対象外にしたり、平均で代用したりなどで誤魔化していましたが、階層ベイズを使えば適切な対処が可能になります。推定の安定性を重視してモデル設計をします。

全体傾向の正確な推定

　実務で運用するケースは少ないですが、学術研究などではこちらの利用用途のほうが多いです。また運用まで至らなくとも、階層ベイズを使う必要があるほど個体差が大きいかを確認するのに使います。

　実務でこのような使い方をすることは少ないのですが、推定自体は難しくないが正確な推定ができるかが問題になる場面で使います。パラメータの安定化では推定の安定性を重視して意図的に柔軟性の低い全体モデルを使うことがありますが、正確な推定を目的とした場合は推定値にバイアスが生じないよう柔軟性の高い全体モデルを使います。

使いどころの判断ポイント

　必要性が低い時に階層ベイズを使っても大変なだけなので、ここでは使いどころの判断ポイントを示します。

ポイント1：個体差が比較的大きい

　個体差がない場合は、個体を区別せずに作成したモデルと同じになります。そのため、個体差が小さくなるほど、階層ベイズモデルは個体を区別せずに作成したモデルに近づいていきます。運用上、個体差を考慮する必要があるほど大きくないのであれば、階層ベイズを使う必要はありません。モデルを運用中に個体差が大きくなるケースを想定して階層ベイズを使うという判断はあるかもしれませんが、階層ベイズにすることで計算量も多くなるので通常は階層ベイスにはしません。

　ユースケースにおいて、個体差が比較的大きいというのは以下の部分に対応しています。

• 例1：企業によって平均提示年収が大きく異なる
• 例2：求人によって採用率が大きく異なる
• 例3：企業によってスキル重視度が大きく異なる

平均提示年収がどの企業でも同じなら全体平均を計算するだけでよいし、採用率がどの求人でも同じなら全体の採用率を計算するだけでよいです。

ポイント2：1個体あたりのデータ量が少ない(ことがある)

　全ての個体について1個体あたりのデータ量が十分にある場合は、階層ベイズモデルは個体別にモデルを作成してその結果を組み合わせたときとほぼ同じになります。1個体あたりのデータ量が増えるほど、全体モデルの影響がなくなるためです。さらに、1個体あたりのデータ量が十分であるならば、各個体のパラメータも安定しやすいため階層ベイズを使う必要性もなくなります。どの程度のデータ量があれば階層ベイズを不要とするかは運用上の必要性に応じて判断しますが、ばらつきの大きいデータであるほど必要なデータ量は多くなります。

　ユースケースにおいて、1個体あたりのデータ量が少ないというのは以下の部分に対応しています。

• 例1：1企業あたりの実績データ数は多いケースも少ないケースもある
• 例2：1求人あたりの応募数は多いケースも少ないケースもある
• 例3：1企業あたりの実績データ数は多いケースも少ないケースもある

データ量が少ないとパラメータを推定するのが難しくなるため、階層ベイズを使ってパラメータを安定化させるのが有効です。

ポイント3：個体差に他の既存データから推定し難い情報がある

　個体差を属性等の既存データから十分正確に推定できるのであれば、データや目的に応じた適切な機械学習手法によって代用できます。階層ベイズを使うのが不適切とは限らないので、選択肢の一つぐらいに捉えるのがよいと思います。しかし、個体差に他の既存データから推定し難い情報が含まれている場合、階層ベイズによる推定結果を既存データと組み合わせて利用すると有効なことがあります。例えば、推定結果を特徴量の一つとして他の属性等と合わせて予測モデルに使うことで精度を上げることができることがあります。

ポイント4：異常値を許容できない

　実務における階層ベイズの一番の利点はパラメータの安定化なので、異常値が算出されても問題ない場合は階層ベイズを使う必要はないことがあります。例えば、人がチェックして判断材料にするような使い方をしているのであれば異常値に気づいて対処できるので異常値をある程度許容できます。一方で、システムに組み込んで重要箇所で使うような場合は異常値があると影響が大きいので階層ベイズが有効になります。

　また、予測問題などでは、異常値があっても全体の予測精度指標などがよいならば問題ないケースでは、必ずしも階層ベイズを使わなくてもよいことがあります。階層ベイズによる予測精度向上は、データ量の少ない個体のパラメータ安定化によるものです。一方で、機械学習の手法によっては異常値を算出することがあるものの全体の精度指標が高くなるものがあります。異常値を許容でき精度指標の高さのみを重視している場合は、そのような機械学習手法を使った方がよいことがあります。

実際の利用場面

　現在事業で使われているものを紹介すると問題があるかもしれないので、以前使われていたものを中心に紹介します。

求人の採用率

　以前運営していた転職ナビという転職サイトでは、求人案件ごとの採用率の推定に利用されていました。中途採用では応募から内定までの期間が長く、採用率を確定させるのに時間がかかるため、採用率推定のニーズが高かったです。採用率は応用範囲が広く、営業だけでなくサイト上での施策でシステマティックに利用される可能性があったので、異常値を抑制し安定した推定値を算出するために階層ベイズを使いました。

　ユースケースの例2に近い形ですが、求人と全体の2階層ではなく、求人と企業と全体の3階層のモデルになっていました。求人別採用率のばらつきが大きいだけでなく、企業別のばらつきも大きかったため、このようなモデルにしました。

　運用開始初期は柔軟かつ安定したモデルを作ったつもりでも、営業施策などによって全体傾向が激変することがあり、その都度モデルを修正していました。データにモデルがフィットしなくなると推定時間が異常に長くなったり推定に失敗したりするので、モデルの修正が必要になります。徐々に、柔軟性を下げ安定性を高めたモデルに作り変えていき、ある程度全体傾向が変化しても動くようにしました。

レコメンデーション

　これも転職ナビの一部で運用されていました。Analytics Blogでもベイズ統計を利用したレコメンデーションをいくつか紹介していますが、運用されていたのはBPMF(Bayesian Probabilistic Matrix Factorization)です。

analytics.livesense.co.jp

　ユースケースの例3に近い形で、データが少ないユーザーや求人の推定パラメータが異常値になるのを抑制するために、階層ベイズが利用されています。転職サイトは同じ人が常に使い続けるサービスではなく求職者が入れ替わっていくためデータが少ないユーザーが多いという特徴があります。そのため、当時運用していた既存のレコメンデーションより高成績でした。

　実運用まで至らず検証レベルでしか使っていないものもありますが、階層ベイズを利用したレコメンデーションモデルの記事を他にも書いているので紹介しておきます。

analytics.livesense.co.jp

analytics.livesense.co.jp

analytics.livesense.co.jp

A/Bテスト・バンディット

　現在も社内で運用しているA/Bテスト基盤では、階層ベイズを利用して結果を評価したりバンディット(Thompson sampling)を実行したりできるようになっていました。具体的には、日別に作成されたCVRの個別モデルと全体モデルで構成されたモデルになっていました。

　ユースケースの例2に近い形ですが、実務では珍しく個別モデルではなく全体傾向の正確な推定を行うための階層ベイズモデルでした。日別でモデルを作成しているのは、システム上データ更新が1日ごとだったことに起因します。

　当時、A/Bテストで有意差が生じた後に結果が逆転するケースがよくみられたことと、バンディットでの初期データへの依存性の高さに対処するために考案したものです。A/Bテストやバンディットでは統計的定常状態であることを仮定するのが一般的です。要するに、KPIの真の値は常に一定であると仮定して、複数日にわたって得られたデータを合算して統計的検定などを行います。しかし、外部環境の影響を受けやすい施策のKPIでは、この仮定が正しくないことがあるのではと考えました。当時入手可能なA/Bテスト結果を集めて日別でKPIが異なっているかを推定したところ、半数程度は日別でKPIが異なっている可能性があることがわかりました。そこで、日別でKPIが変化していても妥当なKPIを推定できるよう階層ベイズモデルをA/Bテスト基盤に組み込みました。

　なお、A/Bテスト基盤に関する過去記事はこちら。

made.livesense.co.jp

　全体傾向の正確な推定を目的とした事例としては、弊社サービス転職ドラフトの提示年収分析でも利用しました。

analytics.livesense.co.jp

紹介型マッチングアプリ

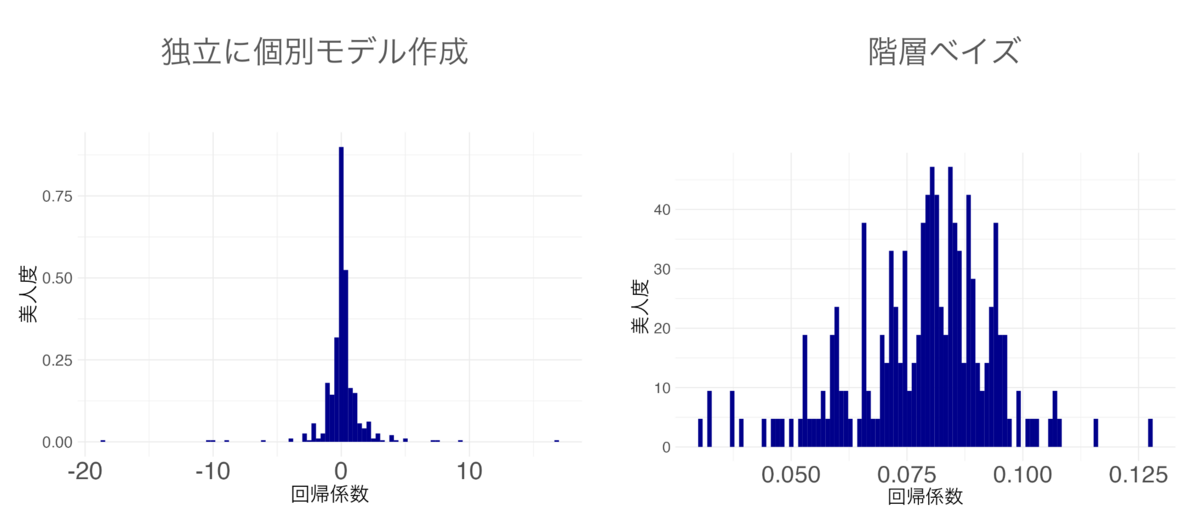
　運用に組み込まれているわけではなくデータ分析での利用にとどまっていますが、紹介型マッチングアプリknewでも、好みの個人差を推定するのに利用しました。ユースケースの例3と同じような使い方です。以下は、容姿の好みを美人度(「かわいい」と「かっこいい・美人」だと「かっこいい・美人」寄りの度合い)で説明するモデルを階層ベイズで作成し、個人別に「かわいい」と「かっこいい・美人」のどちらを好みと評価するかを示したものです。左は階層ベイズを使わずに個人別に推定したときの結果、右が階層ベイズを用いた結果です。ぱっと見、右のグラフのほうがばらけているように見えますが、横軸を比較すると分かる通り階層ベイズを使わないと推定値が安定せず異常な値になっていることがわかります。

紹介型マッチングアプリknewで好みの個人差を推定するのに階層ベイズを使ったときの例（左：階層ベイズなし、右：階層ベイズ）

こちらについては、人工知能学会知識ベース研究会で発表しており、別途記事を執筆予定です。

まとめ

　本記事では、非データサイエンティスト向けに階層ベイズについて紹介しました。階層ベイズを使うことで、個々のデータが少なくてモデル作成が困難な場合でも全体傾向の情報を利用してモデルを作成することができます。階層ベイズの利用用途は「パラメータの安定化」と「全体傾向の正確な推定」の2点で、実務で利用する場合はパラメータの安定化を目的として利用されることが多いです。階層ベイズを使うべきか判断するポイントは「個体差が比較的大きい」「1個体あたりのデータ量が少ない」「個体差に他の既存データから推定し難い情報がある」「異常値を許容できない」の4つで、このような状況で利用するのに適した手法です。データ量が少ないとデータ活用が難しいことが多いのですが、階層ベイズのような手法を使うことで対処できることがあります。